第四次图像信息处理作业解析,这次是图像仿射变换呢。
Assignment-4作业要求
Translation
Rotation
Scale
Shear
Mirror
作业分析
仿射变换简介
图像上的仿射变换, 其实就是图片中的一个像素点,通过某种变换,移动到另外一个地方
从数学上来讲, 就是一个向量空间进行一次线形变换并加上平移向量, 从而变换到另外一个向量空间的过程
向量空间$\vec{m}$:
向量空间$\vec{n}$ :
向量空间从$\vec{m}$到$\vec{n}$的变换 $\vec{n}=A\vec{m}+\vec{b}$
整理得到:
将A跟b 组合在一起就组成了仿射矩阵 $M$。 它的维度是$2∗3$
使用不同的矩阵$M$就获得了不同的2D仿射变换效果。
图像平移
可以说是最简单的空间变换,其矩阵$M$为
因此,我们可以很快地写出代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| uint8_t* imgTranslation(const uint8_t* imgData, int bitCount, int height, int width, int x0, int y0) {
int lineBytesOriginal = (bitCount * width / 8 + 3) / 4 * 4;
int lineBytesTranslated = (bitCount * (width + (int)fabs(x0)) / 8 + 3) / 4 * 4;
uint8_t* transData = new uint8_t[lineBytesTranslated * (height + (int)fabs(y0))]{};
y0 = y0 > 0 ? y0 : 0;
x0 = x0 > 0 ? x0 : 0;
for (int i = 0; i < height; i++) {
for (int j = 0; j < width * 3; j++) {
uint8_t r = *(imgData + i * lineBytesOriginal + j);
j++;
uint8_t g = *(imgData + i * lineBytesOriginal + j);
j++;
uint8_t b = *(imgData + i * lineBytesOriginal + j);
*(transData + (i + y0) * lineBytesTranslated + j - 2 + x0 * 3) = r;
*(transData + (i + y0) * lineBytesTranslated + j - 1 + x0 * 3) = g;
*(transData + (i + y0) * lineBytesTranslated + j + x0 * 3) = b;
}
}
return transData;
}
|
注意变化后bmp文件的header也需要同步变换,在这里给出变化后的header
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| BITMAPHEADER* Header = new BITMAPHEADER;
Header->bfType = 0x4D42;
Header->bfSize = 14 + 40 + lineBytesTranslated * (height + (int)fabs(y0));
Header->bfReserved1 = 0;
Header->bfReserved2 = 0;
Header->bfOffBits = 14 + 40;
BITMAPINFOHEADER* InfoHeader = new BITMAPINFOHEADER;
InfoHeader->biBitCount = 24;
InfoHeader->biClrImportant = 0;
InfoHeader->biClrUsed = 0;
InfoHeader->biCompression = 0;
InfoHeader->biHeight = height + (int)fabs(y0);
InfoHeader->biWidth = width + (int)fabs(x0);
InfoHeader->biPlanes = 1;
InfoHeader->biSize = 40;
InfoHeader->biSizeImage = lineBytesTranslated * (height + (int)fabs(y0));
InfoHeader->biXPelsPerMeter = 0;
InfoHeader->biYPelsPerMeter = 0;
|
向右上平移100像素的效果如图

图像旋转
通过数学推导,我们可以发现,旋转的矩阵$M$如下
这里的$\theta$就是旋转的角度,但是很明显这里是以$(0, 0)$为基础进行的旋转,因此我们需要将我们想要的中心点平移至$(0,0)$再平移回来,即
其中
因此,我们可以推导出$M$有
在代码实现部分,我们需要先确定四个角上的像素坐标,然后再将其规化全为正
1
2
3
4
5
6
7
8
9
10
11
| double radian = theta * PI / 180.0;
int x[4], y[4], cx = *width / 2, cy = *height / 2, xMax = 0, xMin = 0, yMax = 0, yMin = 0;
for (int i = 0; i < *height + 1; i += *height) {
for (int j = 0; j < *width + 1; j += *width) {
x[i / *width + j / *height] = j * cos(radian) - i * sin(radian) + (1 - cos(radian)) * cx + sin(radian) * cy;
xMax = xMax > x[i / *width + j / *height] ? xMax : x[i / *width + j / *height];
xMin = xMin > x[i / *width + j / *height] ? x[i / *width + j / *height] : xMin;
y[i / *width + j / *height] = j * sin(radian) + i * cos(radian) - sin(radian) * cx + (1 - cos(radian)) * cy;
yMax = yMax > y[i / *width + j / *height] ? yMax : y[i / *width + j / *height];
yMin = yMin > y[i / *width + j / *height] ? y[i / *width + j / *height] : yMin; }
}
|
然后我们就可以以此来创建新的宽高的图像,然后根据矩阵一一对应
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int newHeight = yMax - yMin, newWidth = xMax - xMin;
int lineBytesRotated = (bitCount * newWidth / 8 + 3) / 4 * 4;
int lineBytesOriginal = (bitCount * *width / 8 + 3) / 4 * 4;
uint8_t* rotaData = new uint8_t[lineBytesRotated * newHeight]{};
for (int i = 0; i < *height; i++) {
for (int j = 0; j < *width * 3; j++) {
uint8_t r = *(imgData + i * lineBytesOriginal + j);
j++;
uint8_t g = *(imgData + i * lineBytesOriginal + j);
j++;
uint8_t b = *(imgData + i * lineBytesOriginal + j);
int x = j / 3 * cos(radian) - i * sin(radian) + (1 - cos(radian)) * cx + sin(radian) * cy - xMin;
int y = j / 3 * sin(radian) + i * cos(radian) - sin(radian) * cx + (1 - cos(radian)) * cy - yMin;
*(rotaData + y * lineBytesRotated + x * 3) = r;
*(rotaData + y * lineBytesRotated + x * 3 + 1) = g;
*(rotaData + y * lineBytesRotated + x * 3 + 2) = b;
}
}
*height = newHeight;
*width = newWidth;
return rotaData;
|
逆时针旋转45度后效果如图

可以看到图片上有很多黑点,这是因为像素旋转过程中我们舍弃了部分精度导致的,因此我们需要进一步进行插值算法,而插值的方法有很多,我们在这里选择双线性插值
双线性插值
双线性插值利用旋转后图像中的点在原图所对应点周围四个点的数值,在两个方向分别进行线性插值来得到
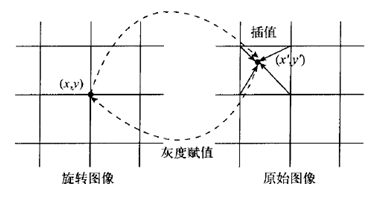
记这四个点分别为$Q_{ij}(i,j=1,2)$,先对x轴方向做两次线性插值得到函数在$R_1$和$R_2$上的值,再对$R_1$和$R_2$做$y$轴方向的线性插值得到函数在所求点的值
而对于旋转的图像,我们先对其变换矩阵$M$求逆运算,其实旋转矩阵的逆即是旋转矩阵的转置,因此
由此我们可以开始插值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| for (int i = 0; i < newHeight; i++) {
for (int j = 0; j < newWidth; j++) {
if (*(rotaData + i * lineBytesRotated + j * 3) == 0 && *(rotaData + i * lineBytesRotated + j * 3 + 1) == 0 && *(rotaData + i * lineBytesRotated + j * 3 + 2) == 0) {
int x = j + xMin, y = i + yMin;
double ox = x * cos(radian) + y * sin(radian) + (1 - cos(radian)) * cx - sin(radian) * cy;
double oy = x * -sin(radian) + y * cos(radian) + sin(radian) * cx + (1 - cos(radian)) * cy;
if (floor(ox) >=0.0 && floor(oy) >=0.0 && ceil(ox) < *width && ceil(oy) < *height) {
int x[2], y[2];
x[0] = floor(ox); x[1] = ceil(ox);
y[0] = floor(oy); y[1] = ceil(oy);
uint8_t r = (y[1] - oy) * (x[1] - ox) * *(imgData + x[0] * 3 + y[0] * lineBytesOriginal) +
(y[1] - oy) * (ox - x[0]) * *(imgData + x[1] * 3 + y[0] * lineBytesOriginal) +
(oy - y[0]) * (x[1] - ox) * *(imgData + x[0] * 3 + y[1] * lineBytesOriginal) +
(oy - y[0]) * (ox - x[0]) * *(imgData + x[1] * 3 + y[1] * lineBytesOriginal);
uint8_t g = (y[1] - oy) * (x[1] - ox) * *(imgData + x[0] * 3 + y[0] * lineBytesOriginal + 1) +
(y[1] - oy) * (ox - x[0]) * *(imgData + x[1] * 3 + y[0] * lineBytesOriginal + 1) +
(oy - y[0]) * (x[1] - ox) * *(imgData + x[0] * 3 + y[1] * lineBytesOriginal + 1) +
(oy - y[0]) * (ox - x[0]) * *(imgData + x[1] * 3 + y[1] * lineBytesOriginal + 1);
uint8_t b = (y[1] - oy) * (x[1] - ox) * *(imgData + x[0] * 3 + y[0] * lineBytesOriginal + 2) +
(y[1] - oy) * (ox - x[0]) * *(imgData + x[1] * 3 + y[0] * lineBytesOriginal + 2) +
(oy - y[0]) * (x[1] - ox) * *(imgData + x[0] * 3 + y[1] * lineBytesOriginal + 2) +
(oy - y[0]) * (ox - x[0]) * *(imgData + x[1] * 3 + y[1] * lineBytesOriginal + 2);
*(rotaData + i * lineBytesRotated + j * 3) = r;
*(rotaData + i * lineBytesRotated + j * 3 + 1) = g;
*(rotaData + i * lineBytesRotated + j * 3 + 2) = b;
}
}
}
}
|
最终效果如图

图像放缩
很明显,这里需要用到上文提到的双线性插值算法,我们在这里换一种写法,相信聪明的你一眼就看出来这两种写法是一样的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| uint8_t* imgScale(const uint8_t* imgData, int bitCount, int height, int width, double ratioA, double ratioB) {
int newHeight = floor(height * ratioA);
int newWidth = floor(width * ratioB);
int lineBytesScaled = (bitCount * newWidth / 8 + 3) / 4 * 4;
int lineBytesOriginal = (bitCount * width / 8 + 3) / 4 * 4;
uint8_t* scaleData = new uint8_t[lineBytesScaled * newHeight];
for (int i = 0; i < newHeight; i++) {
for (int j = 0; j < newWidth; j++) {
double y = i / ratioA;
double x = j / ratioB;
if (y > height - 1) y = height - 1;
if (x > width - 1) x = width - 1;
int x1 = ceil(x), y1 = ceil(y), x2 = ceil(x) + 1, y2 = ceil(y) + 1;
if (x2 > width - 1)
x2 -= 1;
if (y2 > height - 1)
y2 -= 1;
double u = x + 1 - x1;
double v = y + 1 - y1;
uint8_t r = (1 - u) * (1 - v) * *(imgData + x1 * 3 + y1 * lineBytesOriginal) +
(1 - u) * v * *(imgData + x1 * 3 + y2 * lineBytesOriginal) +
u * (1 - v) * *(imgData + x2 * 3 + y1 * lineBytesOriginal) +
u * v * *(imgData + x2 * 3 + y2 * lineBytesOriginal);
uint8_t g = (1 - u) * (1 - v) * *(imgData + x1 * 3 + y1 * lineBytesOriginal + 1) +
(1 - u) * v * *(imgData + x1 * 3 + y2 * lineBytesOriginal + 1) +
u * (1 - v) * *(imgData + x2 * 3 + y1 * lineBytesOriginal + 1) +
u * v * *(imgData + x2 * 3 + y2 * lineBytesOriginal + 1);
uint8_t b = (1 - u) * (1 - v) * *(imgData + x1 * 3 + y1 * lineBytesOriginal + 2) +
(1 - u) * v * *(imgData + x1 * 3 + y2 * lineBytesOriginal + 2) +
u * (1 - v) * *(imgData + x2 * 3 + y1 * lineBytesOriginal + 2) +
u * v * *(imgData + x2 * 3 + y2 * lineBytesOriginal + 2);
*(scaleData + i * lineBytesScaled + j * 3) = r;
*(scaleData + i * lineBytesScaled + j * 3 + 1) = g;
*(scaleData + i * lineBytesScaled + j * 3 + 2) = b;
}
}
return scaleData;
}
|
最终横向拉伸一倍效果如下

图像错切
错切的本质是一种线性变换,可以算是学线性代数的时候的矩阵乘法启蒙变换了吧
对于水平错切,我们有矩阵$M$
其中$m=\tan(\phi)$,也就是说我们将平面上的直线$y=b$错切成了$y=\frac{1}{m}x+b$
很明显,既然有水平错切那就自然有垂直错切,两者在代码上有众多相似之处,因此我们就在这里只实现水平错切
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| uint8_t* imgShear(const uint8_t* imgData, int bitCount, int height, int width, double ratio) {
int newWidth = floor(height * fabs(ratio)) + width;
int lineBytesSheared = (bitCount * newWidth / 8 + 3) / 4 * 4;
int lineBytesOriginal = (bitCount * width / 8 + 3) / 4 * 4;
int offset = 0;
uint8_t* shearData = new uint8_t[lineBytesSheared * height]{};
if (ratio < 0) offset = ratio * height;
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
int y = i;
int x = floor(y * ratio) + j - offset;
uint8_t r = *(imgData + i * lineBytesOriginal + j * 3);
uint8_t g = *(imgData + i * lineBytesOriginal + j * 3 + 1);
uint8_t b = *(imgData + i * lineBytesOriginal + j * 3 + 2);
*(shearData + y * lineBytesSheared + x * 3) = r;
*(shearData + y * lineBytesSheared + x * 3 + 1) = g;
*(shearData + y * lineBytesSheared + x * 3 + 2) = b;
}
}
return shearData;
}
|
值得注意的是,如果比率小于零,那么我们就需要定义一个偏移量offset进行原点偏移,最终结果如下

图像镜像
蛮简单的,没啥好说的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| uint8_t* imgMirror(const uint8_t* imgData, int bitCount, int height, int width, int flag) {
int lineBytes = (bitCount * width / 8 + 3) / 4 * 4;
uint8_t* mirrorData = new uint8_t[lineBytes * height]{};
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
int y,x;
if (flag == 0) {
y = i;
x = width - j - 1;
}
else {
y = height - i - 1;
x = j;
}
uint8_t r = *(imgData + i * lineBytes + j * 3);
uint8_t g = *(imgData + i * lineBytes + j * 3 + 1);
uint8_t b = *(imgData + i * lineBytes + j * 3 + 2);
*(mirrorData + y * lineBytes + x * 3) = r;
*(mirrorData + y * lineBytes + x * 3 + 1) = g;
*(mirrorData + y * lineBytes + x * 3 + 2) = b;
}
}
return mirrorData;
}
|

总结
虽然看上去这次作业也不算特别难,但是在编写代码的过程中我还是遇到了许多奇妙的问题,比如一些公式的笔误导致最终输出的图像根本不能看
而且有的时候图像的分辨率如果恰好是一个奇妙的数值,那么最后输出的图像就有可能会损坏,因此请随意使用本博客里的图像,它的鲁棒性十分的好
总之就是需要胆大心细地按部就班地编写程序,最终就一定会出现自己预想中的图像






