墓碣茶室

Wandleshen的博客

0%

Condition Number for Hilbert Matrix

发表于 更新于
本文字数： 5.9k 阅读时长 ≈ 5 分钟

最近数值分析课遇到一个计算希尔伯特矩阵条件数随维数变化关系情况的问题，在此对其迭代解法的程序实现做一些小小的讨论

希尔伯特矩阵

希尔伯特矩阵是一种系数都是单位分数的方块矩阵，具体来说希尔伯特矩阵的第$i$行$j$列元素为：

因此代码中可以通过双重循环构造矩阵（Golang实现）

1
2
3
4
5
6
7
8
9
10
11
12
13
func genHilbertMatrix(n int) [][]float64 {
	H := make([][]float64, n)
	for i := range H { //初始化矩阵
		H[i] = make([]float64, n)
	}
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			x := float64(i + j + 1)
			H[i][j] = 1.0 / x
		}
	}
	return H
}

求取最大和最小特征值

条件数K的定义为，对于任意范式$||·||$和非奇异矩阵$A$，有

而对于正定矩阵，可以证明条件数为

很明显，希尔伯特矩阵是一个正定矩阵，因此只要求出其最大和最小特征值即可计算出条件数

最大特征值计算

这里我们使用幂法进行计算，注意此时的前提条件为

我们构造一系列向量序列，有

可以证明，

同时在计算机计算过程中，为了防止数据过大导致的越界， 我们可以对$\vec{v_k}$进行规范化，即令

然后对$\vec{u_k}$进行迭代与规范化操作

同时，我们可以证明

因此我们可以得出以下代码来计算最大特征值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func getMaxLambda(mat [][]float64, n int) float64 {
	const MaxIteration = 10000
	const MaxError = 0.00001
	v0 := make([]float64, n) //生成迭代初始向量
	v0[0] = 1.0
	lambda := 0.0
	for lambda0, counter := 1.0, 1; math.Abs(lambda-lambda0) > MaxError && counter < MaxIteration; counter++ { //迭代边界，次数限制与误差限制
		lambda0 = lambda
		u := make([]float64, n)  //生成迭代后向量
		for i := 0; i < n; i++ { //计算u=Av
			u[i] = 0.0
			for j := 0; j < n; j++ {
				u[i] += mat[i][j] * v0[j]
			}
		}
		lambda = 0.0
		for i := 0; i < n; i++ { //找到最大值
			if lambda < math.Abs(u[i]) {
				lambda = math.Abs(u[i])
			}
		}
		for i := 0; i < n; i++ { //进行规范化
			v0[i] = u[i] / lambda
		}
	}
	return lambda
}

计算最小特征值

幂法十分完美地解决了最大特征值的问题，而对于最小特征值，我们可以很自然的想到只要求取$A^{-1}$的最大特征值，其倒数就是原矩阵的最小特征值
但这依然有些麻烦，因此我们可以使用$LU$分解绕过对$A$求逆的过程进行迭代，即通过解方程组：

即可通过$\vec{v}$得出$\vec{u}$的值

$LU$分解

事实上，将$A$进行初等行变换之后变成一个上三角矩阵，其变换矩阵就是一个下三角矩阵，这就是所谓$LU$分解

我们可以通过所谓杜尔利特算法进行分解，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func LUDecomposition(mat [][]float64, n int) ([][]float64, [][]float64) {
	L, U := make([][]float64, n), make([][]float64, n)
	for i := range mat {
		L[i], U[i] = make([]float64, n), make([]float64, n)
	}
	for i := 0; i < n; i++ {
		L[i][i] = 1
		if i == 0 {
			U[0][0] = mat[0][0]
			for j := 1; j < n; j++ {
				U[0][j] = mat[0][j]
				L[j][0] = mat[0][j] / U[0][0]
			}
		} else {
			for j := i; j < n; j++ { //生成U
				temp := 0.0
				for k := 0; k < i; k++ {
					temp += L[i][k] * U[k][j]
				}
				U[i][j] = mat[i][j] - temp
			}
			for j := i + 1; j < n; j++ { //生成L
				temp := 0.0
				for k := 0; k < i; k++ {
					temp += L[j][k] * U[k][i]
				}
				L[j][i] = (mat[j][i] - temp) / U[i][i]
			}
		}
	}
	return L, U
}

回到最小特征值计算

得到了$LU$矩阵，我们只需要反解出$\vec{u}$的值即可迭代到我们需要的精度，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func getMinLambda(mat [][]float64, n int) float64 {
	const MaxIteration = 10000
	const MaxError = 0.00001
	L, U := LUDecomposition(mat, n)
	v0 := make([]float64, n) //生成迭代初始向量
	v0[0] = 1.0
	lambda := 0.0
	for lambda0, counter := 1.0, 1; math.Abs(lambda-lambda0) > MaxError && counter < MaxIteration; counter++ { //迭代边界，次数限制与误差限制
		lambda0 = lambda
		w := make([]float64, n)
		u := make([]float64, n)
		for i := 0; i < n; i++ { //解出Lw=v
			temp := 0.0
			for j := 0; j < i; j++ {
				temp += L[i][j] * w[j]
			}
			w[i] = v0[i] - temp
		}
		for i := n - 1; i > -1; i-- { //解出Uu=w
			temp := 0.0
			for j := i; j < n; j++ {
				temp += U[i][j] * u[j]
			}
			u[i] = (w[i] - temp) / U[i][i]
		}
		lambda = 0.0
		for i := 0; i < n; i++ { //找到最大值
			if lambda < math.Abs(u[i]) {
				lambda = math.Abs(u[i])
			}
		}
		for i := 0; i < n; i++ { //进行规范化
			v0[i] = u[i] / lambda
		}
	}
	return lambda
}

计算条件数

有了上面的前置工作，最后一步计算条件数就显得十分简单，不过我们在$getMinLambda()$中返回的是最小特征值的倒数，因此在最后直接两者相乘即可，最后代码如下

1
2
3
4
5
6
7
func condNum(n int) float64 {
	mat := genHilbertMatrix(n)
	lambda1 := getMaxLambda(mat, n)
	lambda2 := getMinLambda(mat, n)
	cond := lambda1 * lambda2
	return cond
}

运行结果

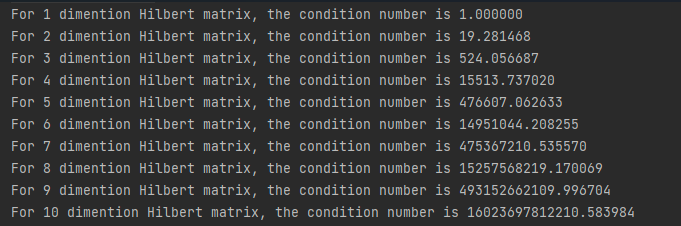
通过与matlab输出进行对比，发现数据精度能达到四到五位

无穷范数情况下的条件数

之前通过特征值对于条件数的计算都是建立在2范数的情况下的，而本题讨论的其实是在无穷范数情况下的条件数变化（审题不清orz）

所幸，我们发现希尔伯特矩阵的逆矩阵可以通过特定公式来求解，即

很明显，他是对称的，所以我们可以省下一半时间计算他们

但是显然，倘若通过阶乘式来求组合数十分容易溢出，故我们可以使用辗转相除法来不断约化防止溢出

1
2
3
4
5
6
7
8
9
10
11
12
13
func gcd(a, b int) int { //求最大公因数
	if b == 0 {
		return a
	}
	return gcd(b, a % b)
}

func div(a, b int) (int, int) { //约化a和b
	gcd := gcd(a, b)
	a /= gcd
	b /= gcd
	return a, b
}

最后我们就可以开始计算组合数了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func combination(n, k int) int {
	i := k + 1
	r := n - k
	if r > k { //选择更少计算量的那一边
		i = r + 1
		r = k
	}
	f1, f2 := 1, 1 //分数的上下项
	j := 1
	for ; i <= n; i++ {
		f1 *= i
		for ; j <= r; j++ {
			f2 *= j
			if f2 > f1 { //分母要小于分子啦~
				j++
				break
			}
			if gcd := gcd(f1, f2); gcd > 1 { //计算中约化
				f1, f2 = div(f1, f2)
			}
		}
	}
	return f1 / f2
}

根据上文提到的公式，我们可以通过编程求出逆希尔伯特矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func genInvHilbertMatrix(n int) [][]float64 {
	invH := make([][]float64, n)
	for i := range invH { //初始化矩阵
		invH[i] = make([]float64, n)
	}
	for i := 0; i < n; i++ {
		for j := 0; j < i + 1; j++ { //根据对称性减少一半计算量
			x := (i + j + 1) * combination(n+i, n-j-1) * combination(n+j, n-i-1) * combination(i+j, i) * combination(i+j, j)
			if (i+j)%2 == 0 {
				invH[i][j], invH[j][i] = float64(x), float64(x)
			} else {
				invH[i][j], invH[j][i] = float64(-x), float64(-x)
			}
		}
	}
	return invH
}

求无穷范数

无穷范数，就是矩阵中绝对值和最大的一行，这个重复性操作可以很简单地用循环实现，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func condNumInf(n int) float64 {
	mat := genHilbertMatrix(n)
	invMat := genInvHilbertMatrix(n)
	normInf1, normInf2 := 0.0, 0.0
	for i := 0; i < n; i++ {
		sum1, sum2 := 0.0, 0.0
		for j := 0; j < n; j++ {
			sum1 += math.Abs(mat[i][j])
			sum2 += math.Abs(invMat[i][j])
		}
		if sum1 > normInf1 {
			normInf1 = sum1
		}
		if sum2 > normInf2 {
			normInf2 = sum2
		}
	}
	return normInf1 * normInf2
}

运行结果

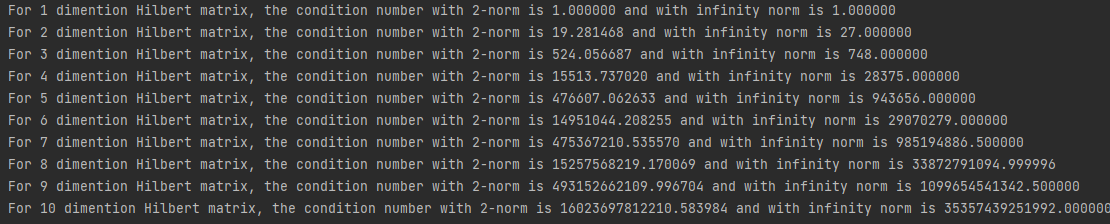
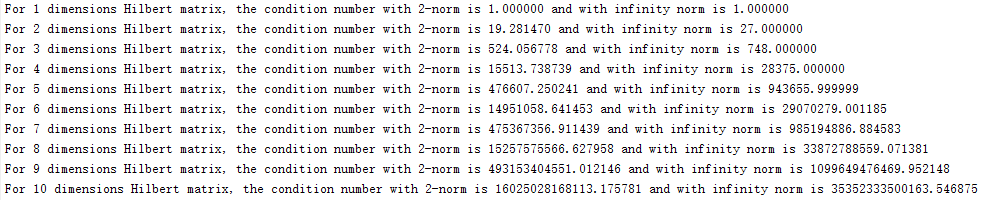
通过与matlab输出进行对比，发现数据精度能达到四到五位